jaumedoa

Divisió de fraccions

«Per què per dividir fraccions hem de multiplicar en creu?»

Hi ha diverses maneres d’explicar perquè «multiplicar en creu» funciona per dividir fraccions. He fet una petita exploració però m’he trobat amb que la majoria de demostracions són molt poc visuals, impliquen formulació massa complicada, o generalitzen les conclusions d’un cas concret.

La idea que més m’ha agradat a l’hora de demostrar visualment la divisió de fraccions ha estat la que proposa Fawn Nguyen una entrada del seu blog Finding Ways. L’únic inconvenient (si ho podem dir així) és que no me quedava clar com podia fer evident la norma de «multiplicar en creu» a l’alumnat a partir del procediment gràfic de divisió que es proposa en el blog. Això és el que intento fer a continuació amb un exemple!

Volem fer la següent divisió:

\qquad \displaystyle \frac{6}{7} : \frac{2}{5}

Aplicant la formula directament:

\qquad \displaystyle \frac{6}{7} : \frac{2}{5} = \frac{6\cdot 5}{7\cdot 2} = \frac{30}{14} = \frac{15}{7} = 2\frac{1}{7}

Gràficament:

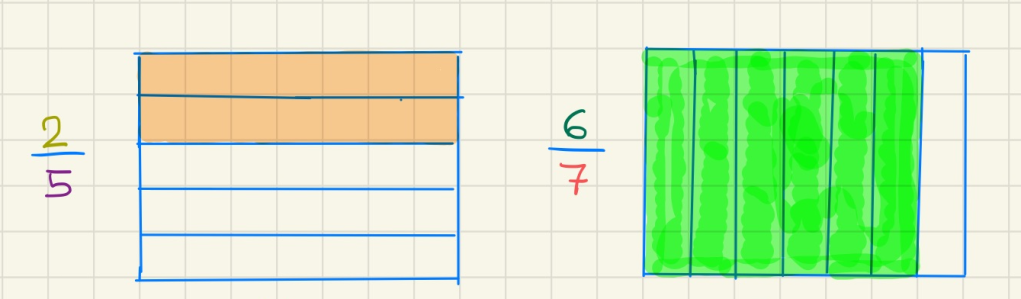
1r pas) Representam \displaystyle \frac{2}{5} i \displaystyle \frac{6}{7}

Per representar gràficament les dues fraccions, dibuixam en una graella un rectangle de mides 5 \times 7 (cada una de les dimensions correspon a un denominador).

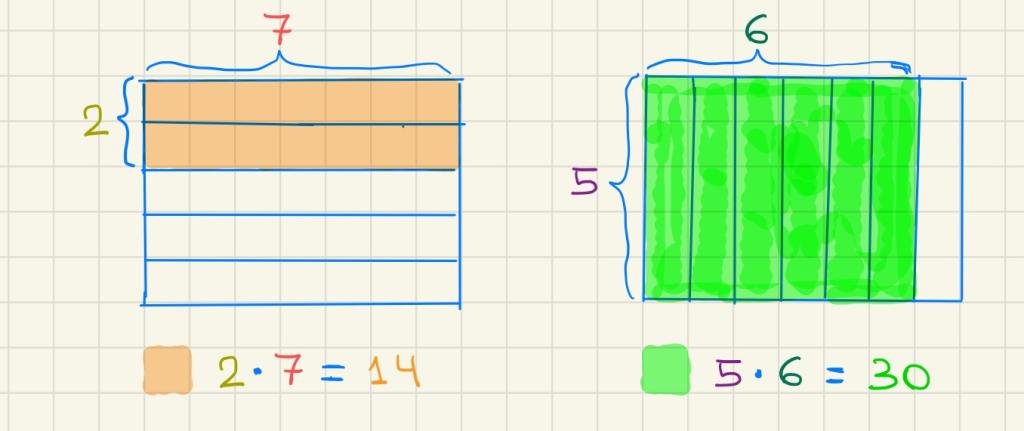
2n pas) Calculam quants quadrets ocupa \displaystyle \frac{2}{5} i \displaystyle \frac{6}{7}

Com que \displaystyle \frac{2}{5} ocupa 2 files (numerador del divisor) de 7 quadrets (denominador del dividend), en total ocupa 2 \cdot 7 = 14 quadrets. Per altra banda, com que \displaystyle \frac{6}{7} ocupa 6 columnes (numerador del dividend) de 5 quadrets (denominador del divisor), en total ocupa 6 \cdot 5 = 30 quadrets.

Ep! Estam «multiplicant en creu» per saber quants de quadrets del rectangle ocupa cada una de les fraccions!

3r pas) Dividim:

Què vol dir dividir \displaystyle \frac{6}{7} entre \displaystyle \frac{2}{5}? Vol dir calcular quants de grups de \displaystyle \frac{2}{5} puc fer amb \displaystyle \frac{6}{7}. Per tant, de manera equivalent, significa calcular quants de grups de 14 puc fer amb 30 quadrets?

Una fracció representa una divisió i, conseqüentment, la resposta serà que puc fer \displaystyle \frac{30}{14} grups, o dit d’altres maneres:

\displaystyle \frac{30}{14} = \frac{6 \cdot 5}{7 \cdot 2} = 2 \frac{2}{14}=2 \frac{1}{7}

Per tant, per dividir fraccions podem «multiplicar en creu»!

És important mencionar que aquest procediment també «funciona» i és intuïtiu encara que el dividend sigui més petit que el divisor, i també per fraccions impròpies! A més, aquesta demostració pot ajudar a que l’alumnat comprengui que la idea que hi ha darrera la divisió de fraccions, que sembla una cosa molt abstracta, és la mateixa que hi ha a l’hora de dividir nombres naturals o decimals.

A veure si funciona quan ho porti a l’aula de 1r d’ESO! Ja vos contaré!

Deja un comentario